| Step of Proof: nat_ind_a |
9,38 |
|
Inference at * 1
Iof proof for Lemma nat ind a:
1. P : 


 {k}
{k}
2. P(0)
3.  i:
i:
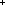 . P(i - 1)
. P(i - 1) 
 P(i)
P(i)
4. i : 
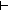 P(i)
P(i)
 by ((((((D 4)
by ((((((D 4)
 CollapseTHENM (IntInd 4))
CollapseTHENM (IntInd 4)) )
)
 CollapseTHENM (D 0))
CollapseTHENM (D 0)) )
)
 CollapseTHENA (
CollapseTHENA (
 C(Auto_aux (first_nat 1:n) ((first_nat 1:n),(first_nat 3:n)) (first_tok :t) inil_term)))
C(Auto_aux (first_nat 1:n) ((first_nat 1:n),(first_nat 3:n)) (first_tok :t) inil_term)))
 C1:
C1:
 C1: 4. i :
C1: 4. i : 
 C1: 5. i < 0
C1: 5. i < 0
 C1: 6. ((i + 1)
C1: 6. ((i + 1) 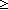 0 )
0 ) 
 P(i + 1)
P(i + 1)
 C1: 7. i
C1: 7. i 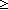 0
0
 C1:
C1: 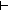 P(i)
P(i)
 C2:
C2:
 C2: 4. 0
C2: 4. 0 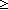 0
0
 C2:
C2: 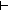 P(0)
P(0)
 C3:
C3:
 C3: 4. i :
C3: 4. i : 
 C3: 5. 0 < i
C3: 5. 0 < i
 C3: 6. ((i - 1)
C3: 6. ((i - 1) 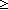 0 )
0 ) 
 P(i - 1)
P(i - 1)
 C3: 7. i
C3: 7. i 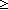 0
0
 C3:
C3: 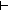 P(i)
P(i)
 C.
C.